Blog
←Voltar
Teoria de Carteiras - Parte 1
Ano 2, No 52
Carlos Martins: Profissional de Investimento Certificado APIMEC CNPI, autor do livro "Os Supersinais da Análise Técnica" (Ed. CampusElsevier, 2010) e sóciofundador do Trader Gráfico.
Carlos Martins: Profissional de Investimento Certificado APIMEC CNPI, autor do livro "Os Supersinais da Análise Técnica" (Ed. CampusElsevier, 2010) e sóciofundador do Trader Gráfico.
Esta semana começamos um assunto muito importante, mas pouco dominado entre os investidores pessoa física, a Teoria de Carteiras ou Teoria de Portfolio.
Em 1952, Harry Markowitz mudou o mundo financeiro ao publicar a sua tese de doutorado Portfolio Selection: Efficient Diversification of Investiment, mais conhecida hoje como Moderna Teoria de Carteiras. Este trabalho, como grande parte dos trabalhos brilhantes, foi muito criticado na época de seu lançamento, pois tratava-se de um tratamento estatístico de diversos ativos com o objetivo de escolher a melhor carteira possível.
Por ter muita estatística associada ao trabalho, muitos se recusavam a ver a teoria por trás dos cálculos. Teoria esta que foi reconhecida em 1990, quarenta anos após o lançamento da tese e do livro de mesmo nome, com o prêmio Nobel de Economia concedido a Harry Markowitz.
O objetivo da Teoria de Carteiras é, principalmente, escolher ativos para uma carteira que tenham uma boa relação risco X retorno. A teoria faz isto calculando sempre o menor risco possível para a carteira como um todo, ponderando a participação de cada ativo, o seu risco e a sua correlação.
Vamos começar entendendo a diferença entre o retorno e o risco. O retorno de uma carteira, aquilo que todos querem aumentar, é diretamente proporcional aos ativos que a integram. Por exemplo, se uma carteira possui dois ativos, o AtivoA e o AtivoB, o retorno da carteira será igual à média ponderada dos retornos de cada ativo em relação ao seu peso na carteira. Veja:
Retorno AtivoA = 10%
Retorno AtivoB = 20%
Se os dois ativos possuírem a mesma participação na carteira, ou seja, 50% para cada, o Retorno da Carteira será:
Retorno da Carteira = (0,5 * 10%) + (0,5 * 20%) = 15%
Agora, se mudarmos a participação dos ativos de modo que o AtivoA tenha 30% de participação e o AtivoB tenha 70%, teremos:
Retorno da Carteira = (0,3 * 10%) + (0,7 * 20%) = 17%
Podemos alterar as participações dos ativos na carteira o quanto quisermos e o retorno geral da carteira estará sempre relacionado com o percentual de participação de cada um.
Já o risco é a incerteza embutida nos retornos esperados. Ele pode ser medido como o desvio padrão das variações percentuais diárias de cada ativo durante um certo período de tempo. Por exemplo, se o Ibovespa sobe 1% hoje, cai -2% amanhã, depois sobe novamente 0,4% e assim por diante, nós pegamos esta seqüência de números e calculamos o seu desvio padrão, assim teremos o risco médio diário do Ibovespa.
A grande novidade na Teoria de Carteiras é que o risco geral da Carteira é menor do que a média ponderada dos riscos de cada ativo que a compõe. Isto por que os riscos de cada ativo não andam juntos, ou seja, no dia em que o AtivoA subir, o AtivoB pode cair e isto deixa o risco da carteira próximo a zero, bem menor do que os riscos individuais.
Claro que isto só é possível se os ativos que compõe a carteira oscilarem de forma independente. Quando dois ativos variam juntos, por exemplo, quando um sobe 1% o outro também sobe 1%, dizemos que a correlação entre eles é 1. Quando dois ativos variam perfeitamente de forma inversa, por exemplo, quando um sobe 2% o outro cai -2%, dizemos que a sua correlação é -1. E todas as outras possilibidades de variação fazem com que a correlação entre os ativos oscile entre -1 e +1.
A correlação entre dois ativos é dada pela fórmula:
Correlação entre A e B = Covariância entre A e B / (Desv.Padrão A x Desv.Padrão B)
A Teoria de Carteiras calcula o risco geral da carteira baseando-se na probabilidade de ativos diferentes, com riscos diferentes, oscilarem de forma independente, ou parcialmente independente, entre si. Isto cria o efeito citado acima, quando um ativo oscila para cima e outro oscila para baixo a carteira acaba oscilando próximo a zero. Sendo assim, quanto mais ativos diferentes e independentes uma carteira possuir, menor será a sua fronteira eficiente de risco.
O cálculo do risco da carteira não é simples, quanto mais ativos na carteira, maior a fórmula que calcula o seu risco, pois é necessário cruzar todos os ativos entre si, um por um, para chegar ao resultado final. Abaixo a fórmula para uma carteira com apenas dois ativos:
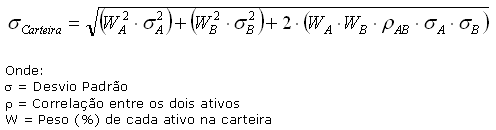
O desvio padrão representa o risco. Na próxima semana explicaremos como calcular o risco da carteira para três ou mais ativos e como incorporar ativos livres de risco em uma carteira.
Em 1952, Harry Markowitz mudou o mundo financeiro ao publicar a sua tese de doutorado Portfolio Selection: Efficient Diversification of Investiment, mais conhecida hoje como Moderna Teoria de Carteiras. Este trabalho, como grande parte dos trabalhos brilhantes, foi muito criticado na época de seu lançamento, pois tratava-se de um tratamento estatístico de diversos ativos com o objetivo de escolher a melhor carteira possível.
Por ter muita estatística associada ao trabalho, muitos se recusavam a ver a teoria por trás dos cálculos. Teoria esta que foi reconhecida em 1990, quarenta anos após o lançamento da tese e do livro de mesmo nome, com o prêmio Nobel de Economia concedido a Harry Markowitz.
O objetivo da Teoria de Carteiras é, principalmente, escolher ativos para uma carteira que tenham uma boa relação risco X retorno. A teoria faz isto calculando sempre o menor risco possível para a carteira como um todo, ponderando a participação de cada ativo, o seu risco e a sua correlação.
Vamos começar entendendo a diferença entre o retorno e o risco. O retorno de uma carteira, aquilo que todos querem aumentar, é diretamente proporcional aos ativos que a integram. Por exemplo, se uma carteira possui dois ativos, o AtivoA e o AtivoB, o retorno da carteira será igual à média ponderada dos retornos de cada ativo em relação ao seu peso na carteira. Veja:
Retorno AtivoA = 10%
Retorno AtivoB = 20%
Se os dois ativos possuírem a mesma participação na carteira, ou seja, 50% para cada, o Retorno da Carteira será:
Retorno da Carteira = (0,5 * 10%) + (0,5 * 20%) = 15%
Agora, se mudarmos a participação dos ativos de modo que o AtivoA tenha 30% de participação e o AtivoB tenha 70%, teremos:
Retorno da Carteira = (0,3 * 10%) + (0,7 * 20%) = 17%
Podemos alterar as participações dos ativos na carteira o quanto quisermos e o retorno geral da carteira estará sempre relacionado com o percentual de participação de cada um.
Já o risco é a incerteza embutida nos retornos esperados. Ele pode ser medido como o desvio padrão das variações percentuais diárias de cada ativo durante um certo período de tempo. Por exemplo, se o Ibovespa sobe 1% hoje, cai -2% amanhã, depois sobe novamente 0,4% e assim por diante, nós pegamos esta seqüência de números e calculamos o seu desvio padrão, assim teremos o risco médio diário do Ibovespa.
A grande novidade na Teoria de Carteiras é que o risco geral da Carteira é menor do que a média ponderada dos riscos de cada ativo que a compõe. Isto por que os riscos de cada ativo não andam juntos, ou seja, no dia em que o AtivoA subir, o AtivoB pode cair e isto deixa o risco da carteira próximo a zero, bem menor do que os riscos individuais.
Claro que isto só é possível se os ativos que compõe a carteira oscilarem de forma independente. Quando dois ativos variam juntos, por exemplo, quando um sobe 1% o outro também sobe 1%, dizemos que a correlação entre eles é 1. Quando dois ativos variam perfeitamente de forma inversa, por exemplo, quando um sobe 2% o outro cai -2%, dizemos que a sua correlação é -1. E todas as outras possilibidades de variação fazem com que a correlação entre os ativos oscile entre -1 e +1.
A correlação entre dois ativos é dada pela fórmula:
Correlação entre A e B = Covariância entre A e B / (Desv.Padrão A x Desv.Padrão B)
A Teoria de Carteiras calcula o risco geral da carteira baseando-se na probabilidade de ativos diferentes, com riscos diferentes, oscilarem de forma independente, ou parcialmente independente, entre si. Isto cria o efeito citado acima, quando um ativo oscila para cima e outro oscila para baixo a carteira acaba oscilando próximo a zero. Sendo assim, quanto mais ativos diferentes e independentes uma carteira possuir, menor será a sua fronteira eficiente de risco.
O cálculo do risco da carteira não é simples, quanto mais ativos na carteira, maior a fórmula que calcula o seu risco, pois é necessário cruzar todos os ativos entre si, um por um, para chegar ao resultado final. Abaixo a fórmula para uma carteira com apenas dois ativos:
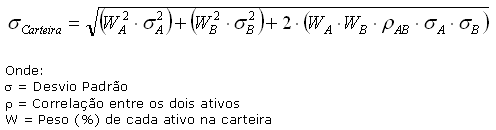
O desvio padrão representa o risco. Na próxima semana explicaremos como calcular o risco da carteira para três ou mais ativos e como incorporar ativos livres de risco em uma carteira.
|
|
O Trader Gráfico possui um simulador de carteiras que sugere o peso de cada ativo escolhido por meio da Teoria de Carteiras. Para fazer as suas próprias simulações sem precisar garimpar os dados estatísticos descritos acima acesse o menu: Minha Carteira > Acompanhar Carteira > Simulação Carteira Clique para ajuda desta função |

